We wanted to make a model in order to test whether simple, reasonable mechanochemical assumptions about the interactions between contractile cortical components suffice to explain three characteristic behaviors of the actomyosin meshwork: spontaneous formation of foci with consistent spacing, formation of the cortex into an anterior cap following weakening at the posterior (presumably by the sperm aster), and smoothening of the cortex following pseudocleavage.
Our data so far suggests that contractile patches of the cortex correspond to regions of high concentrations of actin and myosin. As our experiments progress, we hope to further characterize how actin and myosin interact to cause contractility of the cortex. As a preliminary step in the formation of a model, we keep track of a single molecular species, "actomyosin", which regulates contractility.
In the simulations, we use a radial plot to indicate the concentration of actomyosin in a given cortical segment. Thus, each peak corresponds to one focus, with tall peaks representing big bright foci in the live GFP myosin embryo movies. The ring of peaks is representative of a typical great circle (or great ellipse) of the three-dimensional embryo, as shown below:
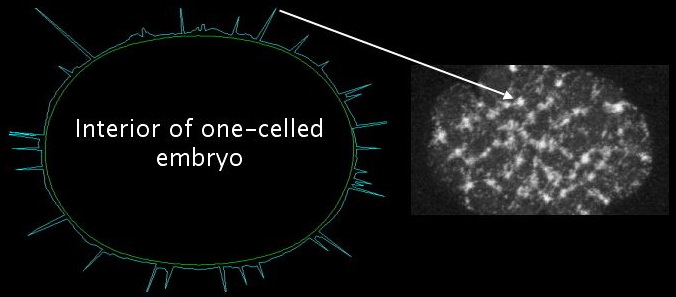
Our model exhibits the formation and disappearance of a consistent number of foci for a given set of parameter values. In addition, these foci merge, just as foci do in the real embryo. By making a simple change in the actomyosin dynamics, we can cause the spontaneous dissolution of the meshwork [movie opens in new window, 820x920 pixels, 14.5 MB]. The correspondence with the real embryo is uncanny, but it is not built in to the model. These behaviors are instead a consequence of reasonable assumptions.
We constructed our model cortex of many discrete elements, each of which behaves like a typical patch of actomyosin meshwork. Such mathematical models involve big calculations to solve the hundreds of simultaneous non-linear differential equations in implicit form.
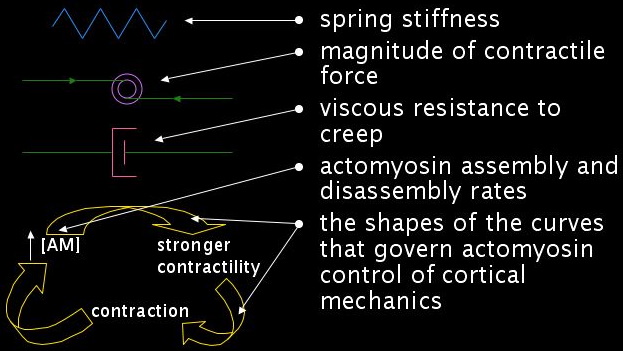
Each discrete segment comprises three elements arranged in parallel: an active contractor, a "creepy spring", and a dashpot. The active contractor generates an insatiable contractile force, mimicking the behavior of myosin. The creepy spring acts in two ways to correspond to a crosslinked actin meshwork: brief application of force yields a simple elastic recoil, just as a Hookean spring would, whereas long-term application of force causes permanent deformation (or creep).
Taken together, the long-term behaviors of the active contractor and the creepy spring are: (1) if the net stretching force is less than the contractile force of the active contractor, the segment will contract forever; (2) if the segment is held at a fixed length, it pulls back with the constant force of the active contractor; and (3) if the net stretching force is greater than the force of the active contractor, the segment will stretch out forever.
The active contractor and the creepy spring alone are not enough to constitute an element because the contraction would occur instantaneously. In order to write down the equations of motion and compute the velocity of a segment, we introduce a viscous drag force proportional to the contraction speed. At the scale of the cytoskeleton, inertial forces are negligible; viscous forces dominate. The viscous drag corresponds, biologically, to the movement of the meshwork relative to the cytoplasm.

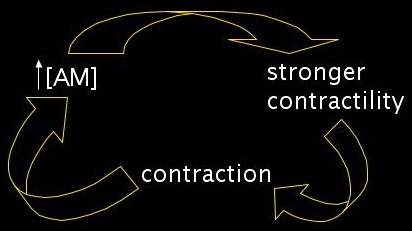
We need to add one more feature. An actomyosin mesh gets stronger if it contracts. A higher density of actin crosslinkers and myosin motors will produce a stronger contractile force. Similarly, stretching out such a mesh should make it weaker. In our segment framework, this constitutes a positive feedback loop. Increased concentrations of actomyosin lead to stronger contractility, which in turn leads to contraction, which further concentrates the actomyosin.
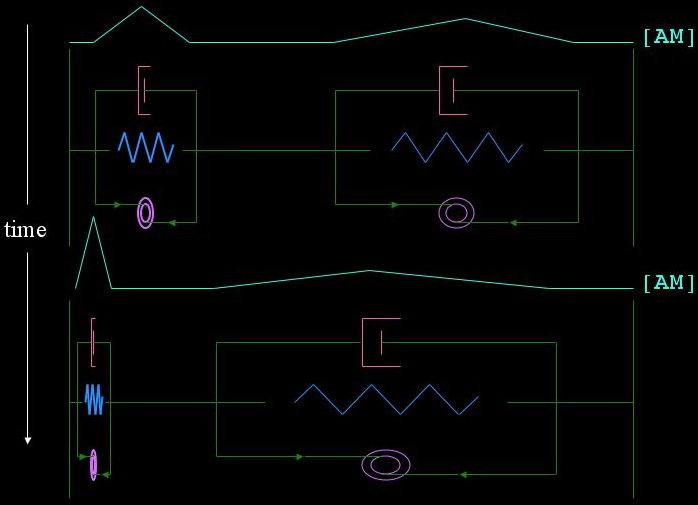
In order to generate intuition about our segments, we can imagine a tug of war. If we have two identical segments pinned at the ends, by making tiny random variations in the initial concentration of actomyosin, we can cause one to win completely if it has the slightest advantage. This scenario is explored in the following diagram. The cyan line indicates the concentration of actomyosin in the two segments; the segment on the left is given an initially higher concentration of actomyosin, and thus will continue to get stronger and more contracted while the segment on the left gets weaker and more stretched out.
Now we would like to populate the entire cortex with such segments, like so:
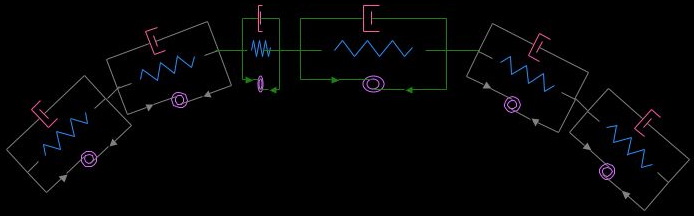
The outcome of inserting our simple tug of war game into a framework with hundreds of identical segments is too hard to intuit. It's time to solve the equations. Herein lies the power of constructing a model. As it turns out, these few simple assumptions are enough, with tiny random variations in the initial concentration of actomyosin, to generate large amplitude deformations that produce foci:
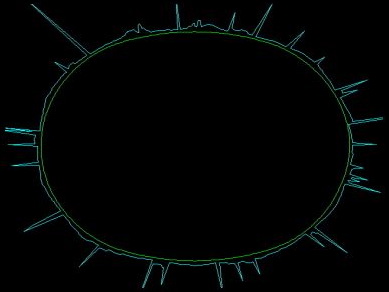
The quantitative behavior of each segment is governed by parameters: the stiffness of the creepy spring, the magnitude of the contractile force of the active contractor, the viscous resistance to creep, actomyosin assembly and disassembly rates, and the shapes of the curves that govern actomyosin control of cortical mechanics. Varying these parameters changes the behavior of the model in two different ways, both of which correspond to variations we observe in the real embryo.
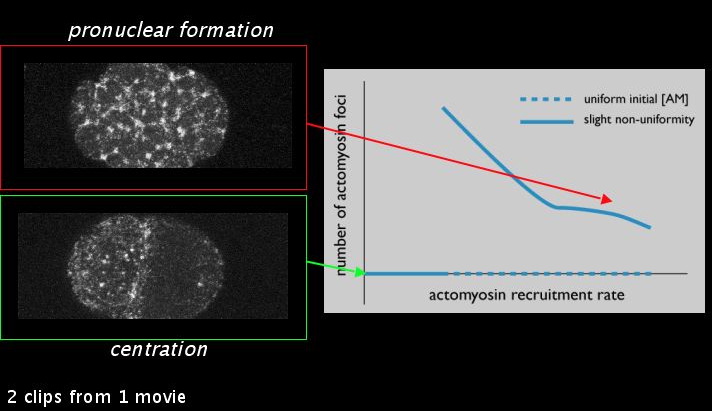
In real embryos, we observe a qualitative difference in the meshwork during pronuclear formation as during centration: during centration, the meshwork formed during pronuclear formation has dissolved into a uniform distribution. Varying the actomyosin recruitment rate alone about a single point is sufficient to explain the dissolution of the meshwork in our model. This parameter is presumably something the embryo might regulate through the PAR or MEX proteins. Graphing the number of actomyosin foci against the actomyosin recruitment rate, we see a bifurcation point where the number of actomyosin foci goes from some to none. This illustrates a general point: in our model, by making a small quantitative change in a parameter, we can generate a qualitatively different behavior.
Our empirical results, described in previous sections on actin organization and myosin dynamics, demonstrate a significant difference in the number of foci across mutants and wild type. Correspondingly, for different parameters, we can change the number of stable foci in our model. We intend to further explore the different parameters that produce this change in the number of foci and see which, if any, generate side effects that correspond to PAR or MEX mutants.
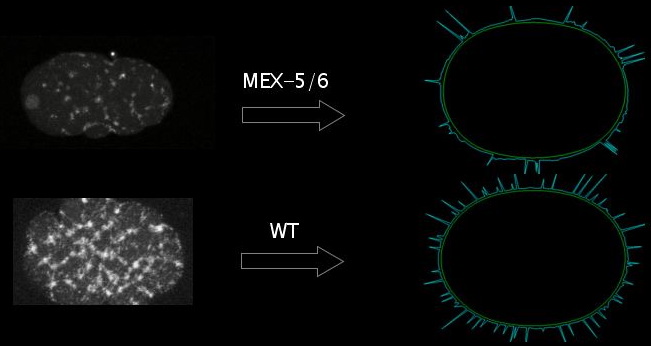
The model demonstrates how assuming that MEX-5/6 or the PAR proteins can change contractility of the cortex could explain different focus dynamics, as our data suggest. These results point to another feedback loop we would like to address in the future: changed contractility and different dynamics of the cortex will move the very cortical proteins that regulate its contractility. The next step in the model is to account for how the moving cortex would transport and concentrate these cortical proteins, with the hope that this might account for protein localization.