Few genes can be said to function "on their own". Rather, most genes can be ascribed a function primarily in the sense that the activities of their product are required for the function of some larger network of interactions among several gene products to produce some sort of higher-order behavior. It is the function and behavior of networks that biologists usually seek to understand. For example, the proteins that regulate cell cycle progression are endowed with various activities (kinases, phosphatases, etc.). Rather than explain their function, much less cell cycle control, by listing the various targets of those activities, biologists are usually after something like an explanation of how all those activities conspire to produce a biochemical oscillator, and how they maintain coordination between the various metabolic and mechano-chemical processes that make up cell growth and division.
Most gene networks are complicated enough that it is a major challenge for humans to use verbal reasoning to envision how the biochemical parts add up to a whole dynamic mechanism of any sort. Furthermore, most naturally-evolved gene networks are so riddled with cross-talk and feedback, and so dependent on non-linear relationships, that the dynamics are very complicated indeed to reason out. It would be nice to do the thought experiment, "If I had an animal (or cell) with only such-and-such a complement of genes, what sorts of behaviors could I expect from it?" One can in principle conduct such an experiment using a computer simulation, assuming one can formulate, with sufficient realism, equations describing how the macromolecular participants react with one another in the context of the cell.
 |
 |
 |
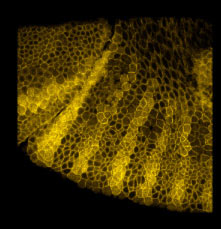
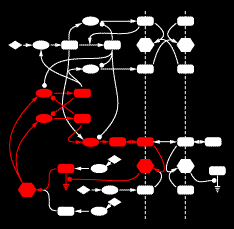
An example gene network dynamics problem: how to account for stripes of segment polarity gene expression in the Drosophila embryo (for instance, the gene Sloppy-paired, shown in the left panel)? Among the known interactions between genes, which ones suffice to account for observed dynamics? The red lines in the middle diagram represent some of the regulatory links between Sloppy-paried and other segment polarity genes that might suffice to explain how this gene is stably maintained in its normal expression domain. All those links have strengths - i.e., parameters governing how strongly each link affects the target - that determine the dynamic behavior of the network. The plot on the right shows sets of parameter values for the red lines in the middle panel which "work", i.e. make stripes; each spoke represents one parameter's range of variation, and the colored lines intersect the spokes at the value for that set. For this simple network some parameters are constrained to particular working ranges. These constraints are predictions about what dynamical rules make the network perform a particular function.
Until recently, few gene networks had been characterized to the extent that one could imagine synthesizing, from the biochemical properties of the individual macromolecules themselves, a computer simulation of the whole mechanisms in which they participate. But over the last decade many well-understood case studies have emerged in a variety of different organisms. In particular, developmental geneticists have probably identified most of the fundamental embryonic pattern-formation circuitry in Drosophila, and described many of the crucial interactions. More important, the especial focus on this one organism means that rather than merely having a "parts catalog" for making a fruitfly, biologists have developed a lot of good ideas about the nature and character of the mechanisms which those parts compose.
For several years we have been developing computer simulations of developmental regulatory gene networks using examples drawn from the extensive literature on Drosophila developmental genetics. One of our goals is to see whether the known facts about the parts catalog actually account for the kinds of mechanisms that biologists have thought up to explain the roles of the genes they study. Another goal is to explore what kinds of systems-level properties emerge that wouldn't have been a foregone conclusion from the properties of the parts alone. Furthermore, by exploring gene networks in simulation we can vary the wiring, the tuning, and constituents, and by doing so learn something about the "design properties" of evolved genetic devices. At the same time we expect the models to educate us about the variational properties of these products of the evolutionary process; "evolvability" and pathogenesis are two sides of the same coin, namely, the tendency for the dynamic behavior of our genetic circuitry to vary in response to mutation or other perturbation.
The first case study we worked on was the Drosophila segment polarity network, which consists of several dozen genes required for segment boundary maintenance during early embryogenesis. This network, or parts thereof, is used in several other contexts during development, many of which involve boundary formation. We like to analogize our gene network model-development approach to the process by which a biochemist might attempt to reconstitute a complex metabolic process like transcription from purified components: we try to add known facts to the simulation and see what kinds of life-like behaviors emerge from the sum of those facts. The facts in question correspond to the kinds of statements that biologists would make when trying to explain how the genetic circuitry works: for example, "the gene engrailed encodes a transcriptional regulator that represses transcription of the sloppy-paired gene", or "the wingless gene encodes a secreted cell-to-cell signal required for engrailed expression", and so on. Obviously "the facts" could be stated at many different levels of detail, and we try to start simple but add details progressively.
|
|
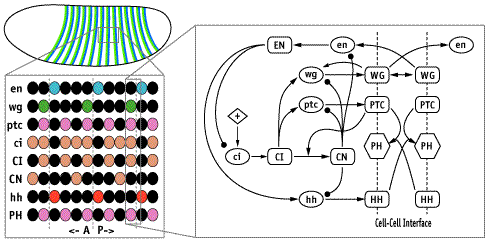
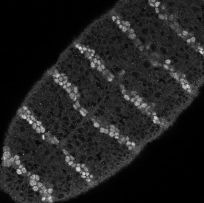
In each segment of the fruit-fly embryo, wingless (wg) is expressed in the row of cells anterior to the parasegmental boundary, and engrailed (en) is expressed in the row posterior. These two cell states are co-dependent during germ band extension, and maintenance of this pattern depends on the function of hedgehog (hh), cubitus interruptus (ci), and patched (ptc), and many other genes. These five, whose pattern of expression is stereotyped on the left and whose regulatory interactions are diagrammed in the center, may be the "core" nodes in the network; many other segment polarity genes mediate their interactions or modulate their functions. The network shown is able to reproduce the pattern on the left under an astonishing range of parameter values and initial conditions. The micrograph on the right shows Engrailed expression on the ventral side of an extended germ-band stage fly embryo.
When we began work on the segment polarity network, we suspected that a small sub-set of the known segment polarity genes and their known interactions might be sufficient to account for their essential function during embryogenesis. That is, we expected to be able to reconstitute the characteristic boundary-maintenance behavior of this putative developmental module with just a "core" of the complete network; we expected that the rest of the segment polarity genes would be required to account for how the network could exhibit robustness to various sources of variability. In our initial work we were surprised find that the apparent core of the network already manifested an astonishing degree of robustness to variation in the initial conditions or parameters. In further studies we showed that the network is robust to diverse architectural variations as well - that is, adding links, intercalating components, etc. - and we explained that the model exhibits robustness because it consists of a set of intertwined cell state switches based on cooperative feedback regulation.
The process of developing this model yielded a variety of predictions about the real network, which we are interested in testing. First of all, the robustness of the model is actually a prediction about the real thing: is the real segment polarity network equally robust? Unfortunately this is rather a difficult question to approach. Instead, we have become more interested in testing whether the model accurately predicts the variational tendencies of the real network. In other words, although the model predicts that the basic pattern-forming function of the network is robust to, say, gene dose variation, it also predicts certain sensitivities. One notable example concerns the width of the engrailed expression domain after germ-band extension. Others have reported that at least some cells that initially express engrailed in the blastoderm stage lose engrailed expression as they move away from wingless-expressing cells during germ-band extension. The current model we have has a very hard time turning engrailed off, once engrailed is turned on, unless certain parameters are carefully tuned or engrailed starts out only at a low level. We are curious to resolve this question both empirically and theoretically: is this property of the real network actually sensitive to variation (e.g. gene dose), or can newly-emerging details about the network, when incorporated into the model, patch up the model's defects?
Why should anyone care about the nuances of segmental boundary maintenance in Drosophila embryos? Aside from the many philosophical, intellectual and methodological issues surrounding modeling and developmental mechanisms, there is one paramount reason why this particular detail seems worth pursuing. Homologues of the segment polarity genes are widely conserved throughout the animal kingdom. Indeed, a surprising fraction of human cancers are based on defects in either the wingless signal transduction pathway or the hedgehog signaling pathway (the other major sub-circuit in the segment polarity network). Here we have a computer model, and a famously tractable experimental model, in which we think we might be able to explore the detailed mechanism of these signaling pathways, and hopefully learn something of fundamental value about how they have been designed by the evolutionary process.
Our segment polarity model is described in the following publications:
G. von Dassow, E. Meir, E. M. Munro, and G. M. Odell (2000) The Segment Polarity Network is a Robust Developmental Module. Nature 406: 188-92.
G. von Dassow and G. M. Odell (2002) Architecture and Constraints of the Drosophila Segment Polarity Module: Robust Spatial Patterning Emerges from Intertwined Cell State Switches. J. Exp. Zool. (Mol. Dev. Evol.) 294: 179-215.
One of the best-studied paradigms of cell-cell signaling in development is the selection of neural progenitors in Drosophila embryos and imaginal discs from clusters of equipotent cells by a signaling network centered around the receptor Notch and its ligand Delta. These genes have for many years been thought of as a lateral inhibition circuit. Notch signaling is thought to cause repression of Delta, such that cells exposed to lots of Delta produce less Delta themselves. Thus, the idea is that the cells of the proneural clusters initially have roughly equal potency to form a neuroblast, and roughly equal levels of activity of the Notch-Delta signaling pathway, but that the pathway is rigged such that small differences among neighboring cells get amplified by feedback, until one cell out of the cluster "wins" the competition and the rest are inhibited from following the same fate. The Notch-Delta pathway mediates diverse variations on this theme throughout Drosophila development, and indeed throughout the animal kingdom.
At first it might seem there would be little mystery about how this pathway accomplishes lateral inhibition. Even trivial mathematical models that represent only Notch and Delta proteins explicitly can produce a lateral-inhibition behavior, and even do so robustly with respect to variation in the initial state or reaction rates. However, there is a vigorous debate about the extent to which the lateral inhibition concept really fits the developmental genetic data. Furthermore, there are some real puzzles about the design of the genetic circuitry that actually mediates between Notch signaling and Delta transcriptional regulation. Notably, proneural competence and selection of a neuroblast both depend on the activity of "proneural" genes of the achaete-scute complex, which seem to be wired (through positive feedback) to behave like a cell-state switch. This ought to work against the postulated lateral inhibition mechanism by forcing cells toward one or the other choice based solely on their initial state. In addition the proneural genes seem to activate their own repressors, members of the Enhancer of split complex. This too seems like it ought to work against the proposed lateral inhibition mechanism by keeping cells from making a decision. These considerations made us wonder whether the neurogenic network could possibly perform lateral inhibition robustly, or whether this required exquisitely fine tuning of the parameters governing the network.
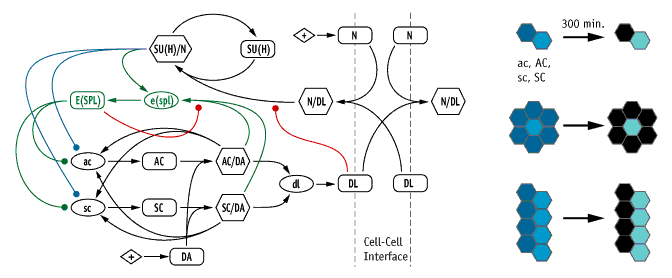
|
Network diagram of our model of the neurogenic/proneural network, in which the genes Notch (N), Delta (Dl), achaete (ac), scute (sc), daughterless (da) Suppressor of Hairless (Su(H)), and Enhancer of Split (E(spl)) are chosen as the critical nodes (left). We tested the ability of this model, and variants based on re-wiring the colored lines, using three geometrically-different lateral inhibition tests (right).
We developed our neurogenic model using a similar approach to the segment polarity model. We found that, as with the segment polarity model, the core neurogenic network can account for lateral inhibition, and that essential function is robust to variation in the parameters governing regulatory interactions. However, building the model granted us what we suspect is a fundamental insight into the mechanism: the combination of a cell-state switch, wrapped in a negative feedback loop, and coupled by extracellular signaling, makes a lateral inhibition circuit that won't go off at the slightest touch, but rather works best with a fairly definite bias between an ordained "winner" and surrounding cells that could make the same choice in the absence of that winner. Our interpretation of the model suggests that the circuit is designed to procrastinate, in effect, until a strong enough cue, either originating from stoachastic variation among cells or an instructive signal, forces the network to make a choice. This interpretation potentially reconciles a variety of competing alternatives with the lateral inhibition model.
Our neurogenic model also provided what we think is a critical insight into evolvability of genetic networks. During development the neurogenic network is deployed in diverse cellular contexts; we stereotyped these into three related tasks for the model network: choosing a winner between two neighboring cells, choosing a winner among a larger cluster of seven cells, and sharpening a boundary between two parallel lines of cells. Each version of the model we tested could accomplish all three of these tasks, given appropriate starting conditions and parameters. Networks tuned so as to be able to robustly perform one of these tasks, could often robustly perform the others as well, if triggered with the appropriate cell geometry and initial conditions. This means that the domains in parameter space that allow each abstract function overlap. This means, in turn, that if Mother Nature invented the network to perform one of these tasks, mutation and selection (even selection for robustness itself, perhaps) could tune the network up to the point that it was capable of performing the others as well. This would not be possible if the network weren't robust in the first place, thus supporting the suggestion put forward by John Gerhart and Marc Kirschner that robustness fosters evolutionary flexibility.
The neurogenic network model is described in:
E. Meir, G. von Dassow, E. M. Munro, and G. M. Odell (2002) Robustness, Flexibility, and the Role of Lateral Inhibition in the Neurogenic Network. Current Biology 12: 778-86.
Most models of genetic networks have approximated networks as haploid, where there is a single version of each gene & gene product. However, the above networks (and other genetic networks studied at the CCD) exist in diploid organisms, and we are constructing diploid versions of these networks. In a diploid network, there are two distinct alleles for each gene that can be identical (if homozygous) or have quantitatively different behavior (a heterozygote with two alleles with slightly different cis/enhancer sequences that are expressed at different levels). This greatly increases the number of interactions in the network as shown below. Imagine a haploid network where two genes, a and b, are transcribed & translated into proteins that bind to form the complex AB, that in turn activates a third gene c. In the diploid case, each gene has 2 distinct alleles, that are made into separate proteins. With 2 versions of each gene, there are 4 possible dimers for AB, each of which could activate the two c's differently.
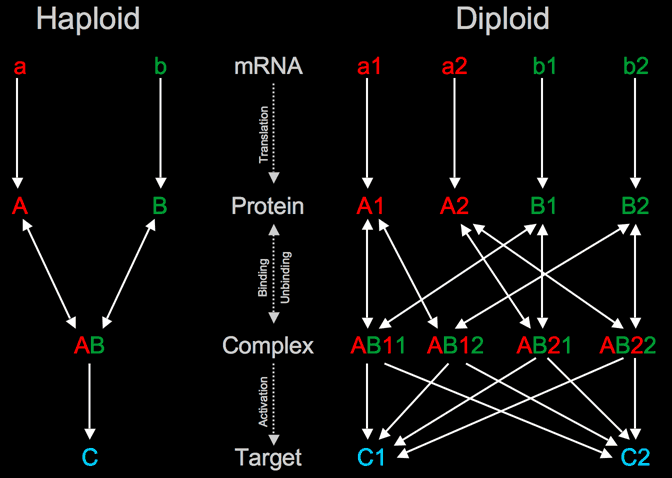 |
Left: Hypothetical haploid network motif consisting of 3 genes. The a and b genes code proteins that activate c when bound to each other. Right: The same network, but diploid so each gene has 2 distinct alleles. This results in a large increase (more than doubling) of the size of the network and number of interactions.
It is unclear for the networks we study whether the increased complexity translates to an increase in robustness due to the redundancy of the network (i.e. mutations are recessive) or whether the increased complexity allows for more possibilities to ruin the network (mutations are dominant). We are constructing models of diploid networks to test whether diploidy confers a robustness advantage at the network level. Additionally, building these diploid networks will allow us to investigate differences between the effects of cis/trans mutations (mutations in transcription factors compared to the enhancer sequences they bind). These networks will also be used to investigate how ploidy influences the evolution of networks.
All our current efforts to model gene networks employ a common mathematical formulation encapsulated in Ingeneue, a general-purpose gene network simulation program. Ingeneue consists of an extensible set of Java class libraries that reads a textual description of a gene network, builds an ordinary differential equation model of the network internally by drawing from a library of formulaic building blocks, runs the simulation (that is, solves the system of differential equations), and conducts various iterative analyses.
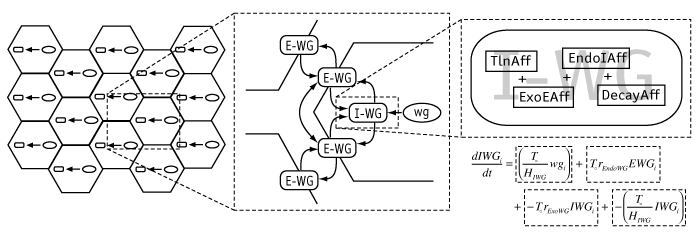
|
The basic modeling framework used in Ingeneue. A two-dimensional grid of cells is populated with identical copies of a gene network, i.e. some nodes and defined interactions among them (left). Nodes represent molecular species; the center panel illustrates this concept with the products of the wingless gene, including an mRNA (wg), an intracellular translation product (I-WG) which exchanges via exo- and endo-cytosis with a secreted form (E-WG) which in turn exchanges with neighboring cells to effect something akin to diffusion. Nodes know how to computed their own rate of change in concentration over time; each one has a list of "Affectors" which represent processes that alter the node's concentration. The right panel shows the Affectors for the I-WG node, which experiences increase due to translation (TlnAff), decrease due to exocytosis (ExoEAff), increase due to endocytosis of E-WG (EndoIAff), and decrease due to first-order decay (DecayAff). The math below shows how Affectors correspond to additive terms in a differential equation, assembled internally by Ingeneue.
Ingeneue is already a useful tool for research (the modeling projects described above used Ingeneue exclusively) and teaching. The principle advantages of Ingeneue over traditional symbolic mathematics software are:
More information about Ingeneue, including the current version, source code, manual, and tutorials, can be found at the Ingeneue website [opens new page]. Also, we published an extensive description of the program itself; please see:
E. Meir, E. M. Munro, G. M. Odell, and G. von Dassow (2002) Ingeneue: a Versatile Tool for Reconstituting Genetic Networks, with Examples from the Segment Polarity Network. J. Exp. Zool. (Mol. Dev. Evol.) 294: 216-51.