(Alberts)
The comprehensive goal is to reproduce, in silico, the various stages of contractile ring formation and ingression from the simplest set of nanoscale rules. This is Occam's Razor from a slightly different viewpoint: we are not using the simplest model --agent-based models are themselves complex-- but we still strive to encode a minimal set of certain and putative interactions to achieve an experimentally observed emergent behavior.
This modeling framework tracks the polymerization, monomer-by-monomer hydrolysis, and depolymerization/severing of actin filaments as they are nucleated by formins bound to protein nodes on the cortex of S. pombe. We thereby formalize, starting with nanoscale interaction rules, the lateral contraction hypothesis for contractile ring formation (Wu et al. 2003; Vavylonis et al. 2008). Protein nodes have a specified number of formins and myosins (and eventually other protein species which may modulate their behavior). Formins nucleate and secure filaments to the nodes --filament release may be force-based or entirely stochastic. Myosin motors are modeled as three-rigid-body machines (see below). Filaments can cross-link to one another and potentially bundle --bundles of actin filaments have increased rigidity, and my be longer-lived than single filaments since the cofilin binding rate can be modulated as a function of bundling interactions.
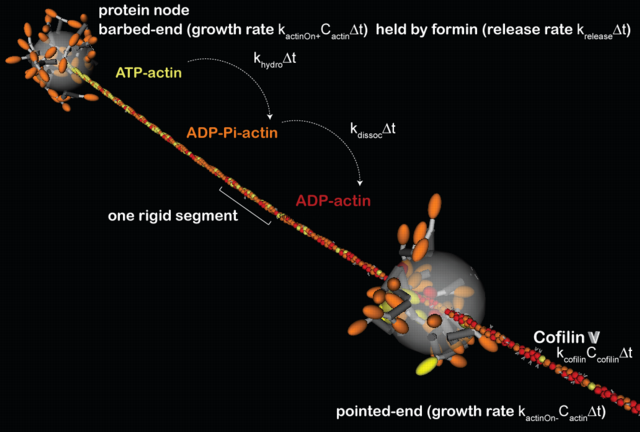
Connected nodes and flavors of actin: One protein node (lower-right) walks on an
formin-nucleated actin filament emanating from another node (upper-left). Colors and markings
on the monomers indicate hydrolysis state and cofilin binding: yellow monomers are ATP-actin,
orange are hydrolyzed ADP-Pi-actin, and red are hydrolyzed and have lost their inorganic
phospate ADP-actin. Cofilin binding to ADP-actin mononmers is indicated by a white carat. To
approximate cofilin mediated actin disassembly, a ratio for cofilin dissolution of an entire
segment is specified, i.e. the entire filament segment is removed from the simulation, and its
monomers returned to the pool of available g-actin, when the number of cofilin decorated
monomers exceeds the specified ratio. Myosin motors on nodes interact with specific monomers on
a filament, and their processivity (i.e. on/off rates) are force modulated. The actin filament
is made from smaller rigid segments (in this case 37-monomers long) connected end-to-end as to
capture biophysical properties of real actin filaments (Alberts 2009). The explicit myosin dimers that populate each node are described in detail below. (Alberts)
In silico actin filaments are assembled from rigid segments (typically 16 to 74 monomers long) that are connected to each other by translational and torsional springs. These springs are tuned to endow these filaments with the appropriate biophysical behaviors (deflection under force, relaxation time-constant, and persistence length, see Alberts PLoSOne, 2009). Flexibility and Brownian motion of filaments effects both the search and capture of nodes during node coalescence, and the stability of contractile rings once formed. See the movies below.

Coalescence of protein nodes: Nodes are initially positioned on
the cortex with a Gaussian distribution about the centroid of the cell. Each formin on the node
(1 formin per node in this case) can nucleate an actin filament and tether it to the node. The
myosin heads on other nodes can grab onto these filaments and thereby pull nodes together. The
parameter set for this particular simulation leads to very transient connections between nodes,
but they nontheless robustly congregate along the cell's equator. (Alberts)
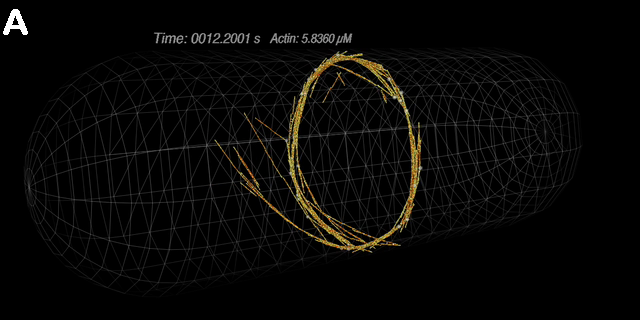
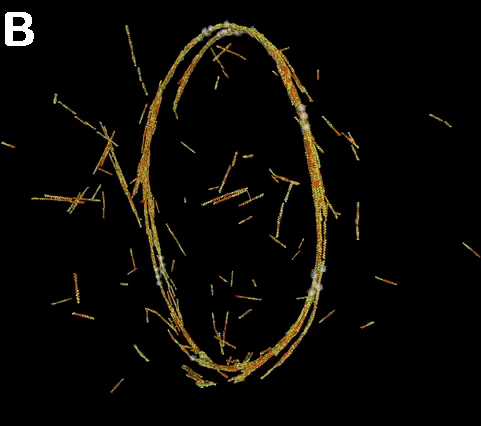
A dynamic ring: A) Nodes initially positioned at the equator are
rapidly joined together by actin filaments. The overall connectivity of this ring structure
is persistent, even though individual filaments come and go. Ring stability, the repositioning of nodes over time, and
the corresponding actin organization, are a few of the issues this model might address. B) A closer look at a similar ring. (Alberts)
The coupling of biochemical- and force-states is nowhere so evident in cell biology as with molecular motors. For actin-binding myosin motor heads, the hydrolysis state (i.e. ATP, ADP-Pi, ADP) of the bound nucleotide, if any, determines the binding affinity for actin filaments and the conformation of the molecule itself. In this way, myosin heads cycle through working- and recovery-strokes while transitioning on and off of actin filaments. Changes in biochemical states can be additionally modulated by external forces, setting up a rich dynamic between motor and cargo. By encoding small-scale feature of myosin motors (e.g. dimensions of tail, neck, and head; explicit biochemical states and transitions for the myosin motor domain) we have a chance to capture some of this dynamic complexity, and can closely tie the model to experimental measurements.
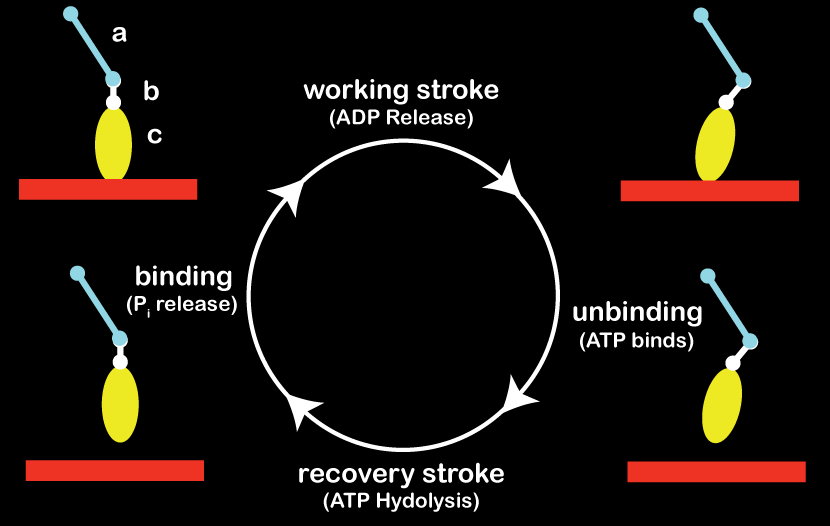
Myosin work cycle: A single myosin in four primary biochemical/conformational states. For
the purposes of our modeling, the motor is idealized as 3 rigid bodies (labeled a:tail,
b:neck, c:head/motor domain) connected by translational and torsional springs. The relaxed
state of those springs (i.e. the preferred conformation of the motor) depends on the
biochemical state of the myosin head. (Alberts)
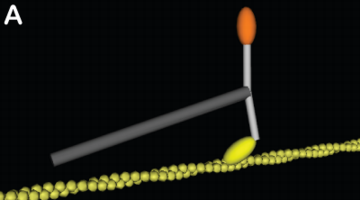
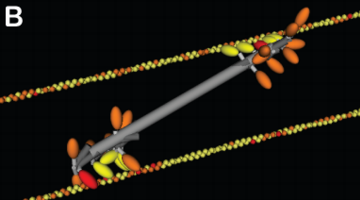
Myosin structures in motion: A) Two myosins with constrained tails and angular contraints on
the neck regions make a dimer. In this case, the geometry of the tail and neck are
representative of myosin V, a processive barbed-end directed motor. B) Many individual myosins
can be arranged into a semblance of a non-muscle myosin minifilament. This minifilament is
exerting forces on antiparallel actin filaments. (Alberts)