Jonathan Alberts and Garrett Odell
Lifelike behavior of a cell arises from interactions among huge numbers of molecules spun from the cell's genes - interactions buffeted by, or brought about by, thermal agitation. How can we get a handle on the cell-level dynamics that emerge from such myriad molecular interactions? We think the best way to understand the molecular genesis of complex cellular behavior is to build detailed computational models that explicitly simulate a large number of biochemical and mechanical interactions among cytoskeletal parts.
Small-scale biological details, which we encode into simple interaction rules, can lead to complex emergent behavior in non-obvious ways. One of our goal is to uncover the dependence of this behavior on molecular interaction details. The behaviors we seek to model in this way are, we believe, 'computationally irreducible'. This means that there isn't a shortcut (i.e. a derivable set of old-fashioned field or continuum equations) that can predict the outcome; we must run ensembles of computer simulations to discover what happens. Our explorations of parametric dependence, and the consequences of changing ratios of different kinds of molecular parts, thus require substantial computational resources; currently, we employ an 80-cpu cluster of computers.
A choice of scale is required in any such model. In other words, we can't really build a single sufficiently detailed model that is useful in simulating any cellular process at any length scale. If we are interested in cell motility should we concern ourselves with the detailed motion and conformation of each individual molecule? When two proteins bind must we calculate the steric transformations by modeling interatomic forces and integrating with femto-second time-steps? Given current computational resources, we forego the world of molecular dynamics and model from a molecular mechanics perspective. Here we represent protein assemblies by their bulk properties. For example, an actin filament is a homogeneous, isotropic, and flexible rod characterized by its length, cross-section, and modulus of elasticity. Actin monomers can attach to (detach from) its ends, but we do not model it as a collection of interacting actin monomers.
At present our most mature computational model addresses bacterial motility. The motility of the Listeria monocytogenes is a popular model system for studying actin network dynamics; we are extending that study with a detailed computational model of the sort described above (see Figure 1). We have also created our own suite of analysis/plotting tools to characterize salient features of bacterial motion - both real and simulated - in order to compare the two.
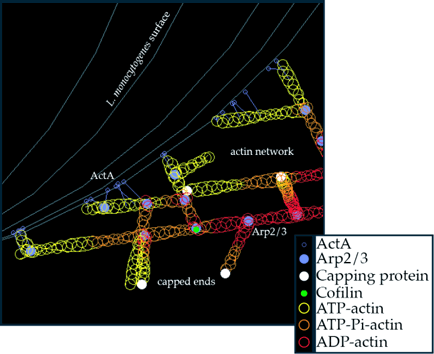
Figure 1. A snapshot of the action near the surface of the bacterium. The legend shows the color code for various players. Lines from ActA to actin filaments indicate transient tethering.
The literature on actin networks and Listeria motility provides a solid experimental base on which to build a realistic simulation. Most key rate constants governing actin network dynamics have been measured (see review Pollard et al 2000). Other work critical to our endeavor includes the identification of the sufficient and necessary proteins for reconstituted motion (Loisel et al, 1999), other biophysical treatments of actin network dynamics (Peskin et al, 1993; Mogilner & Oster, 1996; Mogilner & Oster 2003; Gerbal et al, 2000), and an earlier computational model of actin growth (Carlsson, 2001). Specifically relevant to the work we present in this workshop are biophysical experiments that have revealed discrete step-like motion on the nanometer scale (Kuo & McGrath, 2000; McGrath et al 2003).
Analysis of many simulations with a wide range of key parameter values demonstrates that the observed multi-phasic motion of Listeria, involving discrete steps, pauses, and continuous runs, emerges from cooperative binding and breaking of bonds between actin filaments and the bacteria. Figure 2 shows bacterial position data over a short period of one simulation in which step-like motion emerged. We find it encouraging that such small-scale and unexpected motility details are captured in our simulation.
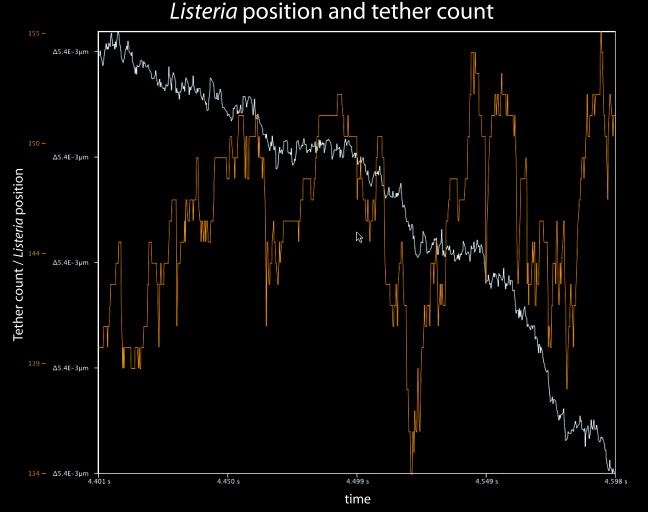
Figure 2. Simulation output showing bacterial position and the number of tethers between ActA proteins and actin filaments. This segment of the simulation demonstrates the salutatory step-like progress of the bacterium.
We are currently developing simulation software, generalizing the Listeria actin polymerization ram, that will allow biologists interactively to specify the mechanical and biochemical interaction properties of numerous cytoskeletal parts such as various filaments such as actin and microtubules, various cross-linkers of these filaments, various motors such as kinesins, dyneins, cytoplasmic myosins, organelles such as nuclei, centrosomes, etc. Our software will constitute the mechanical properties of each small patch of the cortex/plasma membrane bounding a cell from the nearby population of relevant cytoskeletal parts. Simulated cells will contain whatever numbers of the various parts that the user specifies. Our computer programs will then generate the viscous-dominated Newtonian force and torque balance equations for each of the very many cytoskeletal parts and solve them numerically to determine the trajectory through three-dimensional space each part will follow. We simulate the thermal agitation forces that cause Brownian motion. This will provide a computational tool that will allow us and others to perform in silico reconstitution experiments to explore what macroscale behavior might emerge from various ensembles of molecular parts given hypotheses on the pairwise interactions among them. We have preliminary code working well and we are confident that we have solved the difficult computational challenge of detecting every collision between all the parts, each of which is free to move to any location in response to forces that impinge on it. We have implemented a novel scheme to cope with the "infinite stiffness" of our system of ordinary differential equations - stiffness that arises due to sudden collisions between parts. We will show computer-animated movies, typical frames from which appear below, that exhibit the apparently purposeful behavior that emerges from the simple interaction rules we hypothesize.
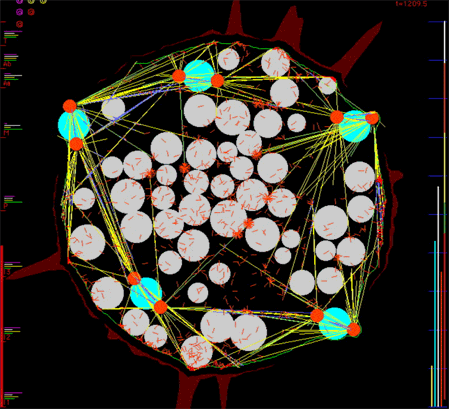
Figure 3. Frame from a movie simulating in 2-D the microtubule-driven migration of nuclei in a syncytial fruit fly embryo, the eruption of cytoplasmic buds as nuclei first reach the cortex, the compaction of yolk particles into the embryo's interior, and the redistribution of filamentous actin in the embryo's cortex.
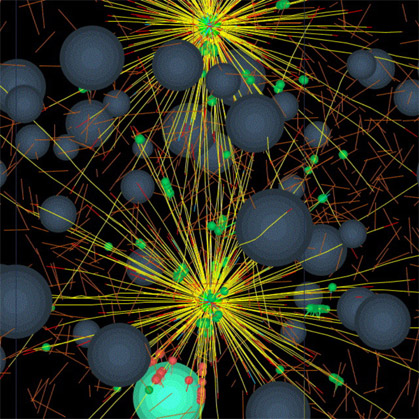
Figure 4. Frame from a proof-of-concept 3-D simulation of a small number of cytoskeletal parts moving each other around. It's Pinocchio just starting to twitch.
There is a profound difference between two-dimensional and three-dimensional models which we will discuss. Preliminary runs of our nascent three-dimensional model, in which we represent only about ten thousand parts, take about 16 hours to run on our fastest dual-processor 2.8Ghz Xeon computer. This extrapolates to an expectation that future realistic runs that involve up to millions of parts would require computer runs that would last many months on single computers. We are therefore developing software to distribute such huge calculations among hundreds of networked processors. These nuts and bolts computer science challenges (which real cells simply ignore as they use their myriad molecules to perform vast computations asynchronously in parallel) are important because the degree to which we succeed in solving them determines how realistic our simulations can be. We will use a significant part of our time to elicit audience opinions about the computational tricks we propose to implement to model the staggering complexity of cytoskeletal dynamics. We seek to learn which of these tricks arouse so much skepticism among biologists that we had best not use them.
cytomechanical modules 2003 • back