Alex Mogilner
Fascinating phenomenon of cell crawling is based on a complex self-organized mechanochemical machine. Migrating cells are polarized, with the cell body at the rear, and a pseudopod - cytoskeletal protrusion largely devoid of organelles - at the front. The dynamic cytoskeletal meshwork of the pseudopod is the basic engine pulling the crawling cell forward [5]. Pseudopodia of many motile cells, such as neutrophils, for example, are characterized by complex shapes and movements, which makes these cells' behavior hard to analyze. On the other hand, some cells possess relatively simple motile appendages and are more suitable to study the motile behavior. For example, fish epidermal keratocytes move steadily and rapidly. Their pseudopod, called lamellipod, has a characteristic 'fan'-like shape. It is few tenths of a micron thick and tens of microns long and wide. Behind the lamellipod is round cell body. The lamellipodial network mainly consists of actin regulated by a host of actin sequestering, capping, severing, nucleating, and depolymerizing proteins, and organized by crosslinking and force generating (myosin) molecules.
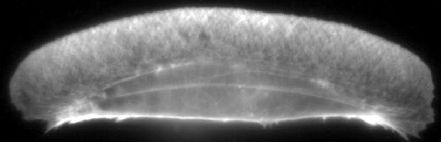
Figure 1: Actin distribution in keratocyte lamellipod. Fish keratocyte stained for Factin with rhodamine phalloidin [1].
Three mechanisms - protrusion, adhesion, and contraction - are acting in concert to produce cell movement. First, growth of the actin plus ends leads to the extension of the cell's leading edge. Then, graded adhesion of the cytoskeleton to the substrate is developed: the adhesion to the surface at the front is firmer, than at the cell's rear. Finally, the actomyosin network contracts, pulling the rear of the cell forward. In keratocytes, all these steps take place simultaneously so that the cells appear to 'glide' steadily without changing its shape.
We concentrate our computational modeling efforts on simple model systems, such as keratocytes, and also Listeria [6] and migrating amoeboid sperm of the nematode Ascaris suum [7]. In this talk we will discuss only protrusion - the best understood part of motility. There are a number of questions about actin based protrusion, where computer modeling can help: What is the nature of the force of protrusion? How is actin recycled from the rear to the front of the cell? What determines the cell shape and migration speed? To answer these questions, we dissect the protrusion phenomenon and analyze first the 'tethered ratchet' model of protrusion force generation. We apply this model to Listeria propulsion and compare its results to recent experimental data. We then discuss the model's implication for lamellipodial extension and discuss future experiments and significance of the adhesion machinery, which could be the limiting factor for protrusion.

Figure 2: 'Tethered ratchet' model of protrusion force generation by Listeria actin tail [2]. The attached (straight) 'mother' filament nucleates/branches a 'daughter' filament. Dissociated 'working filaments' grow, undulate thermally and bend generating elastic force of protrusion (polymerization ratchet). Force balance between the working and attached filaments and the load explain complex force-velocity curve for Listeria. Dendritic nucleation model explains the actin tail organization and actin turnover, however, many quantitative details remain murky.
Then, we turn our attention to the organization of actin in the lamellipod, which is explained qualitatively by the dendritic nucleation model. We examine this model quantitatively and discuss an importance of cytoplasmic convection in actin recycling. We will present preliminary results on combining 'modules' of protrusion to explain the shape and movements of the whole cell and their relations to actin dynamics and organization. We will conclude with discussing many open problems: actin network rheology in vivo, redundancy of mechanical and regulatory pathways, lack of quantitative data, and how computational modeling combined with experimental techniques could accelerate the progress in understanding cell movements.
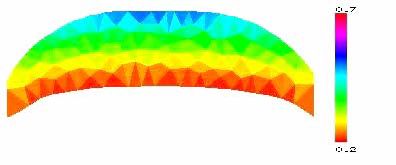
Figure 3: Preliminary results of modeling [3] of steadily migrating keratocyte lamellipodial fragments [4]. The lamellipodial actin network is modeled as a 2-D elastic domain with free boundaries. Finite element method is used to solve equations of mechanics and actin turnover and to move boundaries. Evolved fragment's shape and steady F-actin density are shown.
cytomechanical modules 2003 • back